Справка о
программе "linsolver" (линсолвер)
Системы линейных
алгебраических уравнений (СЛАУ)
встречаются студентами и школьниками на
первых же шагах изучения линейной алгебры и аналитической геометрии. Они являются математическим инструментом решения
задач начертательной геометрии, теории электрических цепей, экономики, теории
упругости, радиотехники и т.д. Широта их применения объясняется тем, что
линейная функциональная зависимость — простейшая математическая модель явлений,
описываемых многими переменными. Более того, методы решения сложных нелинейных
задач, как правило, опираются на пошаговое решение СЛАУ. Таким образом, иметь
простой и удобный инструмент решения СЛАУ типа обычного научного калькулятора
полезно каждому школьнику, студенту, преподавателю, инженеру и научному
работнику.
Система линейных
алгебраических уравнений в общем случае имеет следующий вид:
A[1][1]*X[1] + A[1][2]*X[2] + … A[1][n]*X[n]=Y[1],
A[2][1]*X[1] + A[2][2]*X[2] + … A[2][n]*X[n]=Y[2],
………………………………………………………….
A[m][1]*X[1] +
A[m][2]*X[2] + … A[m][n]*X[n]=Y[m].
Здесь:
n чисел X[1], X[2], … X[n] образуют столбец искомого решения; m чисел Y[1], Y[2], … Y[m] образуют заданный столбец
правой части; числа A[i][j], где i=1, 2, … m,
j=1, 2, … n, образуют главную матрицу системы. Таким образом,
СЛАУ состоит из m линейных уравнений, записанных в m строк, для n неизвестных чисел X[1], X[2], … X[n].
При решении возможны следующие ситуации. Во-первых, в зависимости от заданных главной матрицы системы A и столбца правых частей Y система может иметь
решения и может не иметь ни одного решения. Далее, если система имеет решения,
то
она
либо имеет одно решение, либо имеет бесконечно много решений. Общее решение
СЛАУ, если оно существует, представимо в виде суммы одного частного решения
СЛАУ и общего решения соответствующей однородной системы уравнений с той же
главной матрицей A и нулевым столбцом правых частей Y=0. Однородная СЛАУ имеет в качестве множества
решений линейное подпространство L некоторой размерности k=0,1,2, …n линейного пространства n-мерных числовых
векторов.
Пример
Рассмотрим систему 2
линейных алгебраических уравнений с 3 неизвестными, m=2, n=3, вида
1,5*X[1]
– 0,736* X[2]
+ X[3]=0,
- X[3]=1,37011.
Здесь
главная матрица системы A состоит из 2 строк вида
A[1][1]=1,5; A[1][2]=-0,736; A[1][3]=1;
A[2][1]=0; A[2][2]=0; A[2][3]=-1;
а столбец правых частей состоит из 2 чисел вида
Y[1]=0; Y[2]=1,37011.
Частным
решением этой СЛАУ является столбец из 3 чисел:
X[1]=(-1,37011)/1,5= -0,91340(6); X[2]=0; X[3]= -1,37011.
Соответствующая
однородная система уравнений имеет вид
1,5*X[1]
– 0,736* X[2]
+ X[3]=0,
- X[3]=0.
Множество
всех решений этой однородной системы образует одномерное линейное
подпространство в линейном пространстве всех трёхмерных числовых векторов и
состоит из всех трёхмерных числовых векторов вида
X[1]=(0,736/1,5)*λ; X[2]= λ ; X[3]= 0;
где
λ —
произвольное действительное число.
Программа линсолвер предназначена для решения системы m линейных алгебраических уравнений с n неизвестными вида AX=Y. Здесь A — матрица из m строк и n столбцов, Y — столбец правых частей размерности m, X — столбец неизвестных размерности n. Вводятся пользователем главная матрица системы A и столбец правых частей Y. Программа вычисляет столбец решений X. Данная версия 0 программы имеет ограничения n<17, m<17 на число неизвестных и число уравнений. Точность решения — 8 знаков после запятой. Если решение существует, то программа выдаёт 1 решение системы. Если решение не существует, то программа выдаёт сообщение: «Линейная система не имеет решения».
Размер файла программы
"linsolver.exe"
— 567 KB. В
упакованном для пересылки виде заархивированный файл программы "linsolver.zip" имеет размер 254
KB. Программа
не требует инсталляции.
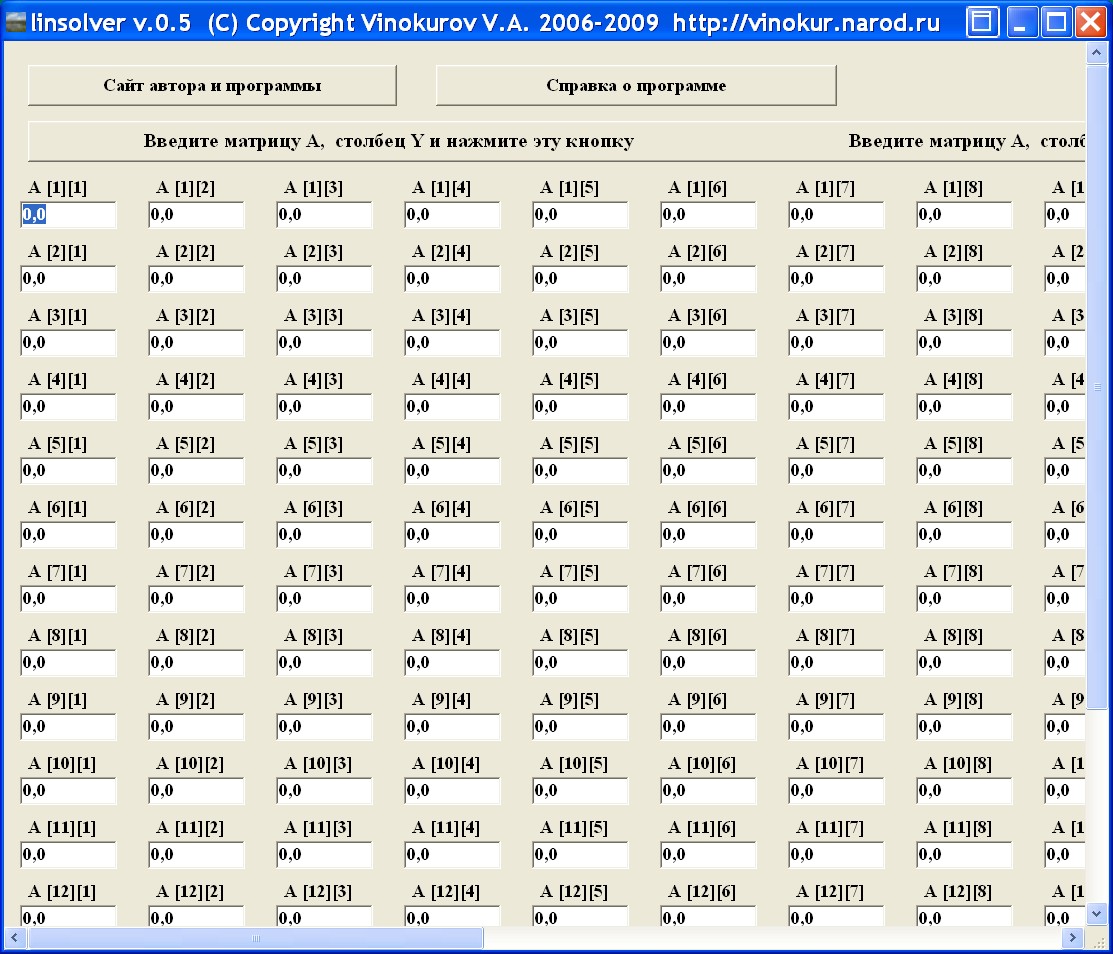
На рисунке внизу Вы
видите окно программы с полями ввода элементов матрицы A и столбца Y (правее матрицы A), и тремя кнопками:
1) главной кнопкой проведения вычислений - "Введите матрицу A, столбец Y и нажмите эту
кнопку",
2) кнопкой вызова справки - "Справка о программе",
3) кнопкой выхода на сайт автора и страницу программы - "Сайт автора и
программы".
Порядок использования программы
1.
Запустите программу из любой директории любого
носителя.
2.
Введите в открывшиеся поля ввода программы ненулевые
элементы матрицы A и столбца Y.
3.
Нажмите кнопку "Введите матрицу A, столбец Y и
нажмите эту кнопку".
4.
В столбце X
прочтите значения решения.
Порядок
действий пользователя для решения рассмотренного выше примера
1. Вводим в
поля ввода ненулевые элементы матрицы A:
A[1][1]=1,5; A[1][2]=-0,736; A[1][3]=1,0; A[2][3]=-1,0
и ненулевые элементы столбца Y:
Y[2]=1,37011.
2. Нажимаем
кнопку "Введите матрицу A, столбец Y и нажмите эту кнопку".
3. Считываем
ответ:
X[1]=0,91340667; X[2]=0,00000000; X[3]=-1,37011000.
Скачать постоянную версию 0.5 - файл "linsolver.zip" размер 325 KB
Адрес автора для вопросов, отзывов и
замечаний:
vinokur@narod.ru